Metode Hukum II Newton dan Lagrange
Thursday, 9 March 2017
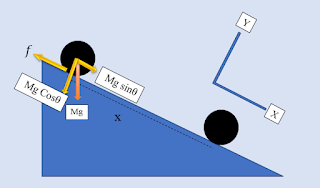
Sebuah benda berbentuk lingkaran bergerak menurunu sebuah bidang miring seperi pada gambar dibawah ini. Jika benda bergerak melingkar dan terdapat gesekan antara benda dan lantai tentukan persamaan gerak benda ?
 |
| Metode Hukum II Newton dan Lagrange |
1. Mengunakan Metode Hukum II Newton
Terjadi 2 Gerakan, Yaitu :
Translasi dan Rotasi
Solusi :
a. Tinjau Gerak Translasi Benda
Dari gambar diatas dapat dilihat bahwa gaya berat Mg terbagi atas dua komponen x,y.
Tinjau Gerak Arah Sumbu Y
∑F_y=m a_y=0 ;Karena tidaka ada perpindaqhan arah sumbu Y
N-m g Cosθ=0
N=m g Cosθ
Tinjau Gerak Arah Sumbu X
∑F_x=m a_x=m a ;dimana a_x=a
m g Sinθ-f=m a………Pers (1)
b. Tinjau Gerak Rotasi Benda
Analisis gaya penyebab benda berotasi dengan mengunakan konsep torsi, dimana penyebab benda berotasi adalah karena adanya gaya gesek antara benda dengan bidang sentuh.
Momen Gaya (Torsi)
τ=r F,dimana gaya yang berkerja adalah gaya gesek (f)
Hubungan Momen gaya dan percepatan sudut
τ=I α ;dimana percepatan sudut benda∶ α=a/R
Dengan menyamakan anata kedua ruas dari persamaan di atas, maka kita peroleh bahwa :
R f=Iα=I a/R ;sehingga di dapatkan besarnya gaya gesek adalah∶
f=I a/R^2 ……….Pers(2)
Subtitusikan Persamaan (2) Ke Persamaan (1), maka diperoleh :
m g Sinθ-f=m a
f=I a/R^2
m g Sinθ-I a/R^2 =m a
Kumpulkan Variabel yang percepatan (a), diperoleh :
a (m+I/R^2 )= m g sinθ
a= (m g sinθ)/((m+I/R^2 ) )
Jadi persamaan gerak benda adalah∶a= (m g sinθ)/((m+I/R^2 ) )
2. Mengunakan Metode Lagrange
Sebelum kita mengunakan metode lagrange maka terlebih dahulu kita mencari informasi mengenai tiga hal berikut ini :
Tentukan Derajat kebebasan : 1 drajat kebebasan (x)
Tentukan Variabel umum : X
Tuliskan persamaan Lagrang : L (x, a, t)
Persamaan Lagrang :
L = T – V
a. Mencari Nilai Energi Kinetik Benda :
Karena benda melakukan dua gerakan, yaitu translasi dan rotasi maka energi kinetik benda adalah energi translasi ditambah energi rotasi :
T=1/2 m x ̇^2+1/2 I ω^2
Dimana : percepatan sudut benda adalah
x=R θ ,maka∶ θ=x/R
Turunkan persamaan diatas terhadap t maka diperoleh :
dθ/dt= ω=x ̇/R
Subtitusikan nilai percepatan sudut ke persamaan diatas, maka diperoleh :
T=1/2 m x ̇^2+1/2 I (x ̇/R)^2
b. Mencari Energi Potensial Benda :
V= -mgh= -mg (x sinθ)
Subtitusikan Kedua persamaan kedalam persamaan lagrange
L = T – V
L=1/2 m x ̇^2+1/2 I (x ̇/R)^2-( -mg (x sinθ))
L=1/2 m x ̇^2+1/2 I (x ̇/R)^2+ mg (x sinθ)
Persamaan Gerak Lagrange :
∂L/∂x- d/dt (∂L/(∂x ̇ ))=0
∂L/∂x= ∂/∂x (1/2 m x ̇^2+1/2 I (x ̇/R)^2+ mg (x sinθ))
∂L/∂x=mg sinθ
∂L/(∂x ̇ )= ∂/(∂x ̇ ) (1/2 m x ̇^2+1/2 I (x ̇/R)^2+ mg (x sinθ))
∂L/(∂x ̇ )=mx ̇+I/R^2 x ̇=(m+I/R^2 ) x ̇
d/dt (∂L/(∂x ̇ ))= d/dt [(m+I/R^2 ) x ̇ ]= (m+I/R^2 ) x ̈
Subtitusian ke dalam persamaan gerak, maka diperoleh :
∂L/∂x- d/dt (∂L/(∂x ̇ ))=0
mg sinθ- (m+I/R^2 ) x ̈=0
(m+I/R^2 ) x ̈=mg sinθ
x ̈= (mg sinθ)/((m+I/R^2 ) )
(d^2 x)/(dt^2 )= a= (mg sinθ)/((m+I/R^2 ) )
Jadi persamaan gerak benda adalah∶a= (m g sinθ)/((m+I/R^2 ) )
Untuk Lebih Jelasnya dapat teman teman download file pdfnya melalui link berikut :
Klik Disini
Jadi dapat dilihat bahwa dengan metode yang berbeda diperoleh hasil yang sama, diman hukum Newton mengunakan konsep gaya yang berkerja pada benda sedankan lagrang mengunakan konsep energi.