Konsep Perkalian Silang (Cross Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan

Pada artikel sebelumnya saya telah menjelaskan tentang Konsep Perkalian Titik (Dot Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan. Nah, untuk kesempatan kali ini saya akan membahas mengenai Konsep Perkalian Silang Dari Dua Vektor atau yang dikenal juga dengan sebutan Cross Product. Simbol perkalian Cross adalah sebuah tanda silang “x”. Di sini kita akan mempelajari tentang bagaimana cara mengalikan 2 Vektor secara Cross dan apa saja sifat yang berlaku pada perkalian ini serta pada bagian akhir kita akan coba mengerjakan contoh soal terkait perkalian silang.

Yang pertama dan perlu di ingat adalah perkalian silang antara dua buah vektor akan menghasilkan sebuah vektor baru. Yang mana besarnya vektor tersebut sama dengan luas daerah yang dilalui oleh kedua vektor. Berbeda dengan Perkalian Titik dari 2 Vektor yang akan menghasilkan sebuah nilai skalar.

Konsep perkalian Cross sering sekali digunakan untuk besaran yang bergerak melingkar, contohnya Medan Magnet (B). Misalkan ketika kita ingin menghitung besarnya medan magnet yang dihasilkan oleh kawat berarus. Maka berdasarkan Hukum Biot Savart, besarnya elemen medan magnet (dB) sebanding dengan besarnya perkalian Cross antara panjang elemen kawat (dl) dan arah vektor satuan (r^), yaitu dB ∝ (dl x r^). Kita tahu bahwa medan magnet selalu bergerak melingkar pada kawan berarus listrik. Contoh besaran lain yang bergerak melingkar adalah Torsi. Dimana besarnya torsi sebanding dengan perkalian Cross antara lengan gaya dan sebuah gaya (r x F).

Perkalian Cross (atau Perkalian Silang) Dari Dua Vektor : (A x B)

Seperti yang telah saya jelaskan perkalian silang dua buah vektor (vektor-vektor) akan menghasilkan sebuah vektor baru yang besarnya sama dengan luas daerah yang dilalui oleh vektor tersebut. Misalkan kita memiliki sebuah vektor A dan Vektor B serta hasil perkalian kedua vektor adalah vektor C maka besarnya vektor C dapat di hitung menggunakan konsep Trigonometri pada sebuah segitiga

Jadi, besarnya vektor C adalah

C = A x B = |A||B| sin θ

Ingat : Hasil perkalian silang dua buah vektor adalah sebuah vektor baru. Karena vektor adalah sebuah besaran yang memiliki nilai dan arah, lalu ke manakah arah dari vektor tersebut?

Misalnya kita masih menggunakan permisalan yang sama, yaitu dua Buah Vektor A dan B yang menghasilkan Vektor C. Maka arah dari vektor C adalah selalu tegak lulus dengan arah bidang yang dibentuk oleh vektor A dan B. Kita misalkan vektor A pada sumbu +x dan vektor B pada sumbu +y maka bidang yang dibentuk oleh vektor A dan B adalah bidang xy. Maka arah yang tegak lurus dengan bidang xy adalah arah sumbu z. Untuk lebih jelasnya maka perhatikan gambar di bawah ini.

Catatan

Karena hasil perkalian dua buah vektor menghasilkan : sin θ. Maka penting untuk mengingat kembali nilai-nilai sin θ pada beberapa sudut. Dan ingat sin θ akan bernilai nol ketika sudut yang dibentuk oleh kedua buah vektor adalah sudut 0 derajat atau kedua vektor searah dan ketika sudut yang dibentuk adalah 180 derajat atau kedua vektor berlawanan arah. Sedangkan, nilai maksimum terjadi ketika kedua vektor tegak lurus atau sudut yang dibentuk 90 derajat.

Searah θ = 0 Maka sin 0 = 0

C = A x B = |A||B| sin 0 = 0

Tegak Lurus θ = 90 Maka sin 90 = 1

C = A x B = |A||B| sin 90 = |A||B|

Berlawanan Arah θ = 180 Maka sin 180 = 0

C = A x B = |A||B| sin 180 = 0

Panjang atau Besar Vektor A adalah |A|

Untuk mencari besar atau panjang vektor maka bisa di dapat dengan cara menjumlahkan kuadrat dari tiap komponen vektor kemudian di akarkan. Atau bisa di sebut sebagai nilai mutlak dari vektor tersebut. Misalnya kita memiliki vektor A dengan komponen vektor pada setiap sumbu koordinat Kartesian 3D (x, y, z).

Perkalian Cross Product Dari Vektor Satuan.

Vektor satuan adalah vektor yang besarnya 1 satuan. Vektor ini menyatakan arah dari sebuah vektor. Ketika dua buah vektor di kalikan secara Cross. Maka perkalian Cross dari dua vektor satuan adalah

Berdasarkan perkalian vektor satuan di atas, maka dapat di simpulkan bahwa jika kita mengalikan vektor A x B = C, maka jika kita mengalikan vektor B x A = -C akan menghasilkan nilai negatif. Jadi : A x B = -B x A

Perkalian Silang Dua Buah Vektor Per Komponen

Misalkan kita memiliki vektor A dan B Tiga Dimensi (3D) dalam koordinat Kartesian (x, y, z). Dan komponen Vektor A adalah (Ax, Ay, Az) sedangkan Komponen vektor B adalah (Bx, By, Bz). Maka ada dua cara dalam menyelesaikan perkalian dua vektor ini secara Cross. Cara yang pertama adalah dengan mengalikan komponen vektor A dan B satu persatu dan Cara kedua yaitu dengan menggunakan determinan matriks.

Cara 1 : Mengalikan Vektor A dan B per komponen

Maka Nilai dari A x B adalah

Kalikan semuanya satu persatu, maka diperoleh

Dari tabel perkalian vektor satuan di atas meka diperoleh

Kemudian kumpulkan komponen vektor dengan vektor satuan yang sama

Cara 2 : Menggunakan Determinan Matrix

Langkah 1 : Cari komponen i, dengan cara tutup bagian i, maka akan tersisa Matrix 2 x 2 dari komponen j dan k. Kemudian hitung determinan Matrix 2 x 2 tersebut, caranya adalah

Perhatikan perbedaan letak elemen matriks jika kita mengalikan j x k dan k x j. Jika kita mengalikan j x k, maka kita juga harus menyesuaikan elemen dalam matriks 2 x 2 pada baris pertama adalah semua komponen j yaitu Ay dan By sedangkan pada baris ke-2 adalah komponen k yaitu Az dan Bz.

Sebaliknya Jika kita mengalikan k x j, maka kita juga harus menyesuaikan elemen dalam matriks 2 x 2 pada baris pertama adalah semua komponen k yaitu Az dan Bz sedangkan pada baris ke-2 adalah komponen j yaitu Ay dan By. Arinya jika kita mengalikan komponen vektor maka kita harus sesuaikan dengan komponen vektor satuan yang mana di kalikan terlebih dahulu.

Langkah 2 : dengan cara yang sama, maka kita per oleh komponen j dan k adalah

Langkah 3 : Gabungkan semua hasil perkalian, maka diperoleh hasil perkalian vektor A dan B adalah

Catatan : Anda tidak perlu membuat perkaliannya satu persatu seperti di atas, di atas hanyalah contoh dan cara saya menjelaskannya kepada Anda. Anda hanya perlu menutup bagian vektor satuan yang ingin kita dan langsung mengalikan determinan matriks.

Contoh Soal dan Pembahasan Perkalian Silang (Cross Product) Dari Dua Vektor

Contoh Soal 1 :

Perhatikan gambar di bawah ini. Sebuah batang besi sepanjang 2 m dan salah satu ujungnya adalah sebagai sumbu putar (Poros). Jika di ujung lainya di beri gaya sebesar 50 N dan gaya tersebut membentuk sudut 30 drajat terhadap batang besi, Maka tentukanlah besar torsi akibat gaya tersebut.

Solusi :

Langkah 1 : Gambarkan gaya-gaya yang bekerja secara vektor. Karena gaya yang bekerja membentuk sudut sebesar 30 deraja maka akan ada komponen gaya yang ke arah sumbu x dan ke arah sumbu y.

Arah vektor r (lengan gaya) adalah dari sumbu putar ke arah kanan. Pada gambar dibawah ini, arah vektor r di gambarkan dengan panah berwarna merah. Sedangkan vektor gaya F di gambarkan dengan anak panah berwarna hitam.

Anak panah berwarna kuning adalah komponen vektor gaya yang mengarah ke sumbu x. Sedangkan anak panah berwarna hijau adalah komponen vektor gaya yang mengerah ke sumbu y.

Tinjau Gaya Fx dan Lengan Gaya

Dari gambar di atas terlihat bahwa komponen vektor gaya Fx berlawanan arah dengan vektor lengan gaya r. Maka nilai torsinya adalah

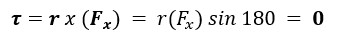
Tinjanu Gaya Fy dan Lengan Gaya

Sedangkan komponen vektor gaya Fy tegak lurus dengan vektor lengan gaya r.

Tanda minus karena arah dari vektor r adalah kearah negatif sumbu x. Dengan acuan koordinat kartesian yang telah kita buat di atas.

Ingat : ketika kita telah menggambar sistem koordinat kartesian maka kita harus konsisten terhadap arah koordinat tersebut.

Dengan demikian, maka diperoleh torsi akibat gaya Fy adalah

Jadi, besarnya torsi akibat gaya tersebut adalah 50 Nm. Tanda negatif k (-k) adalah arah dari torsi tersebut.

Contoh Soal 2

Sebuah gaya yang bekerja pada gagang pintu adalah sama dengan persamaan F = (3 i + j - 2k) N. Jika gaya tersebut bekerja pada gagang pintu yang berjarak r = 2i – j dari poros (sumbu putar). Maka tentukanlah besar dari momen gaya tersebut.

Solusi :

Baca Juga : Bunyi Hukum Charles, Rumus, Contoh Soal dan Penjelasan Lengkap

Itulah artikel tentang Konsep Perkalian Silang (Cross Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan. Semoga artikel ini besar bermanfaat untuk Anda. dan semoga apa yang saya jelaskan bisa dipahami dengan mudah. Jika ada kesalahan dalam penjelasan kami mohon untuk di koreksi agar kami segera memperbaikinya. Terima kasih telah berkunjung dan sampai jumpa kembali.