5 Contoh Soal dan Pembahasan Perkalian Titik (Dot Product) Dari 2 Vektor 3 Dimensi

Contoh soal fisika kelas 10 soal fisika kelas 10 semester 2 soal fisika kelas 10 semester 2 dan pembahasannya latihan soal fisika kelas 10 contoh soal fisika kelas 9 soal fisika kelas 8 semester 2 Latihan soal Fisika kumpulan soal fisika kelas 10 latihan soal fisika kelas 10 semester 2 kumpulan soal fisika smp dan pembahasannya kumpulan soal fisika kelas 11 soal fisika kelas 7 semester 1 latihan soal fisika kelas 12 semester 1 download soal fisika kelas 11.

Gammafisblog.com - 5 Contoh Soal dan Pembahasan Perkalian Titik (Dot Product) Dari 2 Vektor 3 Dimensi. Pada artikel sebelumnya telah saya bahas tentang Konsep Perkalian Titik (Dot Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan. Pada artikel tersebut telah saya jelaskan secara lengkap mengenai apa itu Perkalian Titik atau dalam bahasa inggris “Dot Product”. Perkalian titik, bisa juga disebut dengan perkalian skalar, karena hasil dari perkalian tersebut merupakan sebuah nilai skalar (atau nilai Real). Jika kita melihat secara besaran vektor maka ada dua jenis operasi perkalian vektor, yaitu perkalian titik (Dot Product) dan perkalian silang (Cross Product). Kedua jenis perkalian ini sangat berbeda dan memiliki makna fisis yang berbeda pula.

Jika Anda ingin lebih memahami lagi konsep dari perkalian titik (Dot Product) maka Anda bisa mengeklik link di atas untuk menuju ke artikel tersebut. Karena telah saya bahas secara panjang lebar, maka pada kesempatan kali ini saya hanya akan membahas tentang Contoh Soal dan Pembahasan Perkalian Titik Dari 2 Vektor. Untuk tidak memperpanjang kata langsung saja kita mulai :

Berikut adalah konsep yang perlu Anda mengerti untuk menjawab kumpulan soal di bawah ini.

Konsep Perkalian Titik 2 Vektor

Jika ada dua Vektor A dan B kemudian kedua vektor tersebut di kalikan secara Dot Product maka hasil perkaliannya adalah

A.B=|A||B| cos⁡ θ

θ adalah sudut yang dibentuk oleh kedua vektor dan |A| adalah tanda mutlak dari vektor A yang artinya besar atau panjang dari vektor tersebut. Jika kita mengetahui hasil dari perkalian titik dari kedua vektor dan panjang dari masing-masing vektor maka kita bisa memperoleh besar sudut yang dibentuk oleh kedua vektor tersebut.

Panjang Vektor

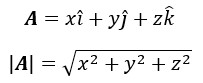
Perkalian Vektor Satuan

Sebuah vektor terdiri dari sebuah nilai dan arah (atau Vektor Satuan). Nilai tersebut menyatakan besar dari vektor tersebut. Arah (atau Vektor satuan) menyatakan ke mana arah dari vektor tersebut pada koordinat.

Vektor 1 Dimensi

Misalkan sebuah vektor r memili besar 2 dan mengarah ke sumbu +x pada koordinat kartesian. Maka kita bisa gambarkan vektor tersebut pada koordinat kartesian sebagai berikut

r = 2i, dimana dua adalah besar atau panjang dari vektor r dan i adalah arah (atau vektor satuan) dari vektor r pada sumbu x.

Jadi, Untuk Vektor 2 Dimensi (r = x i + y j) dan Vektor 3 Dimensi (r = x i + y j + z k). Dimana (x, y, z) menyatakan besar dan (i, j, k) menyatakan arah dari vektor tersebut.

Besarnya perkalian titik (Dot Product) dari dua vektor satuan adalah :

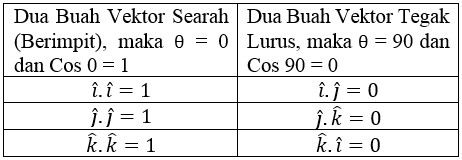
A.B = |A||B| cos ⁡θ

Ingat : Sumbu x akan selalu tegak lurus dengan sumbu y dan z. Begitu juga sumbu y dan z akan selalu tegak lurus dengan sumbu yang lain. Artinya sudut yang dibentuk oleh vektor arah sumbu x dan arah sumbu y sama dengan 90 derajat. Sedangkan Cos 90 = 0, maka i.j = j.k = k.i = 0. Karena sudut yang dibentuk adalah 90.

Baca Juga : Konsep Perkalian Silang (Cross Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan

Perkalian Titik Dua Vektor Per komponen

Misalkan vektor 3 Dimensi dari A dan B. Maka Perkalian Dua Vektor Secara Dot Product adalah:

5 Contoh Soal dan Pembahasan Perkalian Titik (Dot Product) 2 Vektor

Contoh Soal 1:

Dua Buah Vektor A dan B merupakan vektor 3D pada koordinat kartesian. Jika Vektor A = 5i + 3j + 7k dan Vektor B = 12i – 3j + k. Maka tentukan panjang masing-masing Vektor, hasil perkalian titik A.B, dan besar sudut yang dibentuk oleh kedua vektor tersebut.

Solusi :

Diketahui :

A = 5i + 3j + 7k
B = 12i – 3k + k

Ditanya : Panjang Vektor, Hasil Perkalian Titik dan Besar sudut?

Menentukan Panjang atau Besar dari Masing-masing Vektor

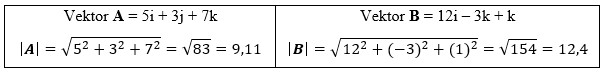
Jadi Panjang Vektor A adalah 9,11. Sedangkan panjang vektor B adalah 12,4

Menentukan Hasil Perkalian Titik

Menentukan Besar Sudut

Jadi, Besar sudut yang dibentuk oleh kedua vektor adalah 83,4 derajat.

Contoh Soal 2

Diketahui sebuah benda diberikan gaya sebesar F = (6i + 3j + 2k) N. Akibat gaya tersebut benda berpindah sejauh r = (8i + 4j) m. Tentukan usaha yang dilakukan oleh gaya tersebut.

Solusi :
Usaha (W) sama dengan besarnya gaya F yang diberikan pada sebuah benda hingga mengakibatkan benda tersebut bergerak sejauh r.

W = F . r = (6i + 3j + 2k).(8i + 4j)

Ingat Konsep perkalian titik dua vektor 3D di atas

Karena vektor r hanya mengarah pada sumbu i dan j maka komponen ke arah k sama dengan nol. Maka

W = F . r = (6.8)+(3.4)+(2.0) = 48 + 12 + 0 = 60 Nm atau 60 Joule

Jadi besarnya usaha akibat gaya tersebut adalah 60 Joule

Contoh Soal 3

Dua buah vektor 3D, yaitu u = 12i + 3j – k dan v = -3i + 2j + ck. Tentukan besar c agar kedua vektor tersebut tegak lurus.

Solusi :

Ingat ketika kedua vektor tegak lurus maka sudut yang dibentuk adalah 90 derajat dan nilai dari cos 90 = 0, maka

Jadi, agar kedua vektor tegak lurus maka nilai c harus sama dengan -30

Contoh Soal 4 :

Dua buah vektor 3D, yaitu u = i + 2j + 3k dan v = 2i + 4j + ck. Tentukan besar c agar kedua vektor tersebut searah.

Solusi :
Ingat ketika kedua vektor searah maka sudut yang dibentuk adalah 0 derajat dan nilai dari cos 0 = 1, maka

u.v = |u||v| cos 0 =|u||v|

Maka terlebih dahulu kita mencari panjang vektor u dan v serta hasil perkalian titik kedua vektor tersebut

Mencari panjang kedua vektor

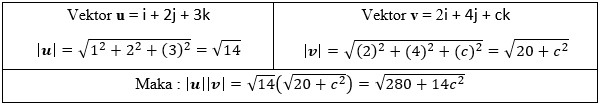
Hasil perkalian Titik Kedua Vektor

Maka diperoleh

Jadi, agar kedua vektor searah maka nilai c harus sama dengan 6

Contoh Soal 5

Dua buah vektor A dan B dimana panjang masing-masing vektor tersebut adalah |A| = 10 dan |B| adalah 18. Jika kedua vektor tersebut membentuk sudut 30 60 drajat satu sama lain, maka tentukan hasil perkalian titik kedua vektor.

Solusi :

A.B = |A||B| cos θ

A.B = 10 (18) cos 30 = 180 (1/2) = 90.

Jadi, hasil perkalian titik atau dot product dari kedua vektor tersebut adalah 90.

Baca Juga : Rangkuman Besaran, Satuan, Dimensi, Vektor dan Skalar Materi Kelas 10 SMA

Itulah artikel tentang 5 Contoh Soal dan Pembahasan Perkalian Titik (Dot Product) Dari 2 Vektor 3 Dimensi. Semoga artikel ini bermanfaat untuk Anda. jangan lupa follow blog ini agar Anda tidak ketinggalan artikel-artikel bermanfaat lainya. Jangan lupa juga untuk share artikel ini kepada teman Anda agar teman Anda tahu apa yang Anda ketahui. Mari berbagi pengetahuan dalam kebaikan. Oke, mungkin itu saja artikel kali ini. Terima kasih telah berkunjung dan sampai jumpa kembali.