5 Contoh Soal Perkalian Silang (Cross Product) dan Pembahasan Lengkap
Saturday, 13 April 2019
Gammafisblog.com - Contoh Soal Perkalian Silang (Cross Product) dan Pembahasan Lengkap. Contoh soal fisika kelas 10 soal fisika kelas 10 semester 2 soal fisika kelas 10 semester 2 dan pembahasannya latihan soal fisika kelas 10 contoh soal fisika kelas 9 soal fisika kelas 8 semester 2 Latihan soal Fisika kumpulan soal fisika kelas 10 latihan soal fisika kelas 10 semester 2 kumpulan soal fisika smp dan pembahasannya kumpulan soal fisika kelas 11 soal fisika kelas 7 semester 1 latihan soal fisika kelas 12 semester 1 download soal fisika kelas 11.

Pada artikel sebelumnya telah kami bahas mengenai Konsep Perkalian Silang (Cross Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan. Nah, pada kesempatan kali ini kami akan membahas mengenai contoh soal perkalian silang dari dua vektor. Di sini Anda akan belajar bagaimana menentukan hasil perkalian dua vektor, besar vektor dan luasan yang dibentuk oleh kedua vektor. Sebelum kita mulai saya harap Anda telah paham mengenai apa itu vektor, besaran vektor, vektor satuan, panjang vektor dan bagaimana cara menentukan hasil perkalian dari dua vektor. Jika Anda belum memahami konsep ini maka saya menyarankan Anda untuk membaca artikel kami yang khusus membahas tentang itu semua. Link artikel ada di atas. Baik, jika Anda sudah membacanya maka langsung saja kita mulai :
Rangkuman Materi Tersebut

Baca Juga : 5 Contoh Soal dan Pembahasan Perkalian Titik (Dot Product) Dari 2 Vektor 3 Dimensi
Contoh Soal Perkalian Silang (Cross Product) dan Pembahasan Lengkap
Contoh Soal 1:
Dua buah vektor memiliki komponen 3D pada sumbu kartesian. Jika vektor A = 2i + 5j + k dan vektor B = -5i + 4j +7k. Tentukan hasil perkalian silang (Cross Product) antara vektor A x B.
Solusi :
Cara 1 : Perkalian Vektor Per Komponen
A x B = (2i + 5j + k) x (-5i + 4j +7k)
A x B = 2(-5)(i x i) + 2(4)(i x j) + 2(7)(i x k) +
5(-5)(j x i) + 5(4)(j x j) + 5(7)(j x k) +
1(-5)(k x i) + 1(4)(k x j) + 1(7)(k x k)
Ingat : Perkalian Vektor Satuan
i x i = j x j = k x k = 0
i x j = k dan j x i = -k
j x k = i dan j x k = -i
k x i = j dan k x i = -j
Maka Hasil Perkalian Silang Antara Kedua Vektor Di atas adalah
A x B = -10 (0) + 8 (k) + 14 (-j) +
(-25)(-k) + 20 (0) + 35 (i) +
(-5) (j) + 4 (-i) + 7 (0)
A x B = (35 i – 4i) + (-5j – 14j) + (8k + 25k)
A x B = 31i – 19j + 33k
Cara 2 : Menggunakan Konsep Perkalian Matriks

Jadi, Kedua cara akan menghasilkan hasil yang saya. Namun cara kedua adalah cara yang paling cepat untuk menyelesaikan perkalian dua vektor.
Contoh Soal 2 :
Sebuah batang besi yang salah satu ujungnya sebagai sumbu putar. Jika panjang besi tersebut adalah 6,71 m Kemudian sebuah gaya F = (2i + 3j + 6k) N diberikan pada batang besi tersebut pada jarak r = (4i + 2j + 5k) m dari pusat sumbu putar. Diketahui bahwa gaya tersebut menyebabkan besi tersebut bergerak melingkar. Tentukan besar torsi yang dialami oleh benda tersebut?
Solusi :
Diketahui :
F = (2i + 3j + 6k) N
r = (4i + 2j + 5k) m
L = 6,71 m
Ditanya : Besar torsi?
Rumus Umum Torsi adalah
τ = r x F
Keterangan Rumus :
τ adalah vektor torsi (Nm)
r adalah lengan gaya (m)
F adalah gaya yang bekerja (N)

Jadi, besar torsi tersebut adalah 16,4 Nm
Contoh soal 3
Sebuah vektor gaya F yang besarnya adalah |F| = 20 N bekerja pada sebuah gagang pintu yang jaraknya 20 cm dari pusat sumbu putar. Jika gaya yang bekerja membentuk sudut 30 drajat terhadap gagang pintu maka tentukan besar torsi yang dialami oleh gagang pintu tersebut.
Solusi :
Diketahui:
|F| = 20 N
|r| = 20 cm = 0,2 m
θ = 30 drajat
Ditanya : Torsi?
Rumus Umum Torsi, Jika yang diketahui sudut dan panjang masing-masing vektor.
τ = r x F ; maka besar torsi tersebut adalah
τ = |r||F| sin θ = (0,2 m) (20 N) sin 30 = 4 (1/2) = 2 Nm
Jadi, besar torsi yang dialami oleh gagang pintu adalah 2 Nm
Contoh Soal 4 :
Jika dua vektor A = i + 2j dan vektor B = 4j + 5k maka tentukan hasil perkalian silang antara vektor A x B dan B x A
Solusi :
Menentukan hasil perkalian vektor A x B

Jadi hasil perkalian vektor A x B = 10i – 5j + 4k
Menentukan hasil perkalian vektor A x B

Jadi hasil perkalian vektor A x B = - (B x A). Sehingga dapat disimpulkan kerikan kita membalikkan perkalian antara 2 vektor misal A x B menjadi B x A maka arah vektor hasil perkalian silang kedua vektor akan berbalik arah atau berlawanan.
Contoh Soal 5:
Diketahui tiga buah vektor A, B, dan C seperti pada gambar di bawah ini. Jika panjang dari masing-masing vektor tersebut berturut-turut 6, 8 dan 10 satuan. Maka tentukanlah besar dari perkalian vektor berikut ini:
a. A x B
b. B x C
c. C x A
Solusi :
a. Menentukan nilai dari A x B
Ingat : Karena vektor tidak memiliki titik awal maka kita bisa pindah vektor tersebut. asalkan kita tidak mengubah nilai dan arah dari vektor tersebut.Perhatikan bahwa sudut yang dibentuk antara vektor A dan B adalah sudut 90 derajat karena kedua vektor tegak lurus. Ingat sin 90 = 1
A x B = |A||B| sin θ
A x B = 6(8) sin 90 = 48
Jadi, Persar dari Perakalian A x B adalah 48
b. Menentukan Nilai dari B x C
Dari gambar di bawah ini dapat kita lihat bahwa sudut yang dibentuk antara kedua vektor adalah 180 – x. Dengan demikian maka kita dapat menentukan nilai dari perkalian kedua vektor tersebut
B x C = |B||C| sin θ
B x C = |B||C| sin (180 – x) = |B||C| sin (x)
Dengan konsep trigonometri pada segitiga siku-siku, maka kita beroleh sin dari sudut x adalah 6/10.
B x C = 8(10) (6/10) = 48
c. Menentukan Nilai dari B x C
Dari gambar di bawah ini dapat kita lihat bahwa sudut yang dibentuk antara kedua vektor adalah 180 – y. Dengan demikian maka kita dapat menentukan nilai dari perkalian kedua vektor tersebut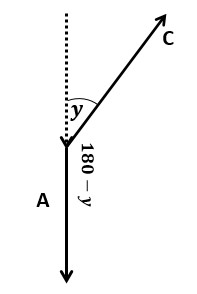
C x A = |C||A| sin θ
C x A = |C||A| sin (180 – y) = |C||A| sin (y)
Dengan konsep trigonometri pada segitiga siku-siku, maka kita beroleh sin dari sudut y adalah 8/10.
C x A = 10(6) (8/10) = 48
Dapat dilihat bahwa perkalian silang dari ketiga kasus di atas menghasilkan nilai yang sama. Hal, ini dikarenakan perkalian silang merupakan luas daerah yang dilalui oleh kedua vektor tersebut. Pada perkalian vektor A x B akan sama dengan luas bangun persegi panjang. Sedangkan pada perkalian B x C dan C x A akan menghasilkan luas yang sama dengan luas jajar genjang. Untuk lebih jelasnya perhatikan gambar di bawah ini

Baca Juga : Konsep Perkalian Titik (Dot Product) Dari Dua Vektor Beserta Contoh Soal dan Pembahasan
Itulah artikel tentang Contoh Soal Perkalian Silang (Cross Product) dan Pembahasan Lengkap. Semoga artikel ini bermanfaat untuk Anda. pada dasarnya perkalian silang akan menghasilkan sebuah vektor baru yang tegak lurus dengan bidang yang dibentuk oleh kedua vektor. Penjelasan di atas ini adalah contoh soal perkalian silang. Untuk materi lengkap tentang perkalian silang telah saya bahas sebelumnya secara lengkap. Anda baiknya Anda membaca artikel tersebut agar bisa lebih memahami contoh soal ini. Link artikel ada pada bagian atas artikel ini pada paragraf pertama. Jika ada pertanyaan silahkan Anda bertanya, karena kami akan coba menjawab pertanyaan Anda sebisa kami. Terima kasih telah berkunjung, semoga Anda nyaman selama membaca artikel kami dan sampai jumpa di artikel bermanfaat selanjutnya.
Contoh soal fisika kelas 10 soal fisika kelas 10 semester 2 soal fisika kelas 10 semester 2 dan pembahasannya latihan soal fisika kelas 10 contoh soal fisika kelas 9 soal fisika kelas 8 semester 2 Latihan soal Fisika kumpulan soal fisika kelas 10 latihan soal fisika kelas 10 semester 2 kumpulan soal fisika smp dan pembahasannya kumpulan soal fisika kelas 11 soal fisika kelas 7 semester 1 latihan soal fisika kelas 12 semester 1 download soal fisika kelas 11.

